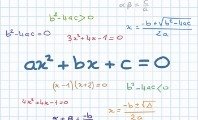Fórmula de Bhaskara: o que é e como se calcula
Fórmula de Bhaskara é um método de resolução da equação do segundo grau, também conhecida como equação quadrática.
Temos, a seguir, a representação da fórmula de Bhaskara, seguida da sua fórmula complementar, a do delta (Δ), chamado também de discriminante:
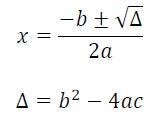
Passo a passo da Fórmula de Bhaskara
Passo 1: Identificação da equação do segundo grau e seus elementos
Define-se como equação do segundo grau ou quadrática a equação ax² + bx + c = 0, sendo que:
-
x é uma variante de valor desconhecido ou incógnita.
- a, b e c são os coeficientes, e a é diferente de zero.
Na equação do segundo grau temos, no primeiro elemento da igualdade, um polinômio de grau dois com uma única incógnita: ax² + bx + c = 0, e é por isso que essa equação recebe esse nome.
Independentemente da ordem dos elementos, em uma equação do segundo grau sempre teremos:
- o coeficiente a (chamado de coeficiente quadrático) acompanhando o termo x²
- o coeficiente b (coeficiente linear) acompanhando o termo x,
- o coeficiente c (coeficiente constante) como o termo independente.
Existem dois tipos de equações do segundo grau: as completas e as incompletas. Equação completa é aquela que possui todos os seus coeficientes diferentes de zero. Quando pelo menos um de seus coeficientes é igual a zero, temos a equação incompleta. A fórmula de Bhaskara é geralmente utilizada para solucionar equações completas.
Exemplos:
- Equação completa: 2x² + 3x - 4 = 0
- Equação incompleta: 9x² - 2 = 0 (o coeficiente b é igual a zero)
São chamadas soluções ou raízes da equação ax² + bx + c = 0 os valores de x que tornam essa equação verdadeira. Uma equação do segundo grau pode possuir no máximo dois números reais ou complexos como raízes.
Passo 2: cálculo do delta (Δ)
Antes de aplicar a formula de Bhaskara, é necessário empregar o cálculo do delta (Δ) ou discriminante:
Δ= b2- 4ac
O valor do Δ indica se a equação possui solução real ou não:
- Com Δ > 0, temos duas soluções reais.
- Com Δ = 0, temos uma única solução real.
- Com Δ < 0, não existe solução real.
Passo 3: aplicação da fórmula
Como exemplo de aplicação da fórmula de Bhaskara, resolveremos a equação 2x² - 5x - 7 = 0:
A forma ax² + bx + c = 0 é chamada forma geral. Comparando a equação dada com a forma geral, temos:
- a = 2
- b = - 5
- c = - 7
a) Cálculo do discriminante:
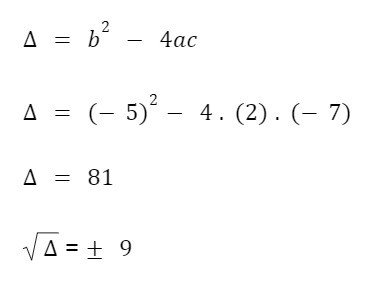
b) Cálculo das raízes pela fórmula de Bhaskara:
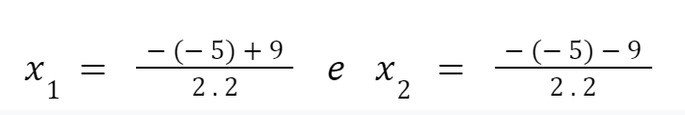
ou seja:
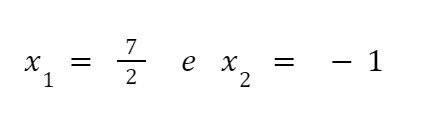
Portanto, a equação 2x² - 5x - 7 = 0 possui as raízes
Fórmula de Bhaskara: uma invenção brasileira
Bhaskara Akaria foi um proeminente matemático indiano do século XII. Mesmo tendo publicado diversos tratados sobre álgebra, não é dele a autoria da fórmula que leva o seu nome. Na verdade, essa fórmula existe há mais de 4000 anos, desde os babilônios. Bem antes dele nascer, portanto.
A expressão "fórmula de Bhaskara" usada para nomear o método resolutivo da equação do segundo grau ou quadrática só existe no Brasil. Acredita-se que deve ter surgido na década de 60 e se difundido por meio dos livros didáticos, que continuam a usar essa nomenclatura até hoje.
A autoria e a motivação dessa homenagem despropositada são desconhecidas.