Conjuntos numéricos
Conjuntos numéricos são grupos de números que compartilham características comuns e são classificados em categorias específicas para facilitar o estudo e a compreensão das propriedades e das relações entre eles.
Estes conjuntos são essenciais na matemática, pois permitem organizar diferentes tipos de números e suas operações de maneira lógica. Os principais conjuntos numéricos são:
-
Conjunto dos números naturais (ℕ): inclui todos os números inteiros não negativos, usados principalmente para contagem. Geralmente, começa do zero ou do um, dependendo da definição. Exemplo:
.
-
Conjunto dos Números Inteiros (ℤ): abrange todos os números naturais, seus opostos (números negativos) e o zero. Por exemplo,
-
Conjunto dos números racionais (ℚ): formado por números que podem ser expressos como uma fração
onde a e b são inteiros e b ≠ 0. Por exemplo,
.
-
Conjunto dos números irracionais (I): inclui números que não podem ser escritos como frações exatas, pois possuem infinitas casas decimais não periódicas. Exemplos:
,
.
-
Conjunto dos números reais (ℝ): formado por todos os números racionais e irracionais, ou seja, todos os números que podem ser representados em uma reta numérica. Exemplo:
.
-
Conjunto dos números complexos (ℂ): abrange números que possuem uma parte real e uma parte imaginária. São representados na forma de
, onde
e
são números reais e
é a unidade imaginária
.
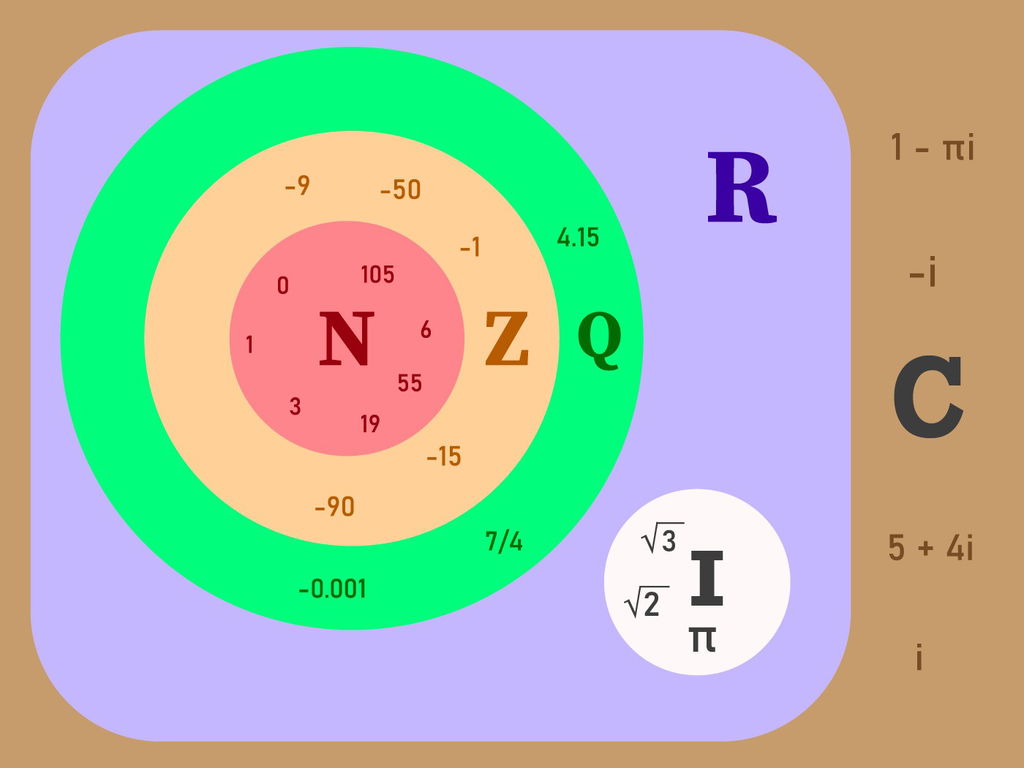
Esses conjuntos são organizados de forma hierárquica, onde os números naturais estão contidos nos inteiros, que estão contidos nos racionais, e assim por diante.
Conjunto dos números naturais (ℕ)
O conjunto dos números naturais (ℕ) é formado pelos números inteiros não negativos e é amplamente utilizado para contagem e ordenação. Ele inclui os números 0, 1, 2, 3 e assim por diante, seguindo infinitamente sem incluir números negativos ou frações.
Todos os elementos deste conjunto são maiores ou iguais a zero, o que significa que ele não inclui números como -1, -2 ou qualquer outro valor abaixo de zero. Além disso, os números naturais são inteiros, ou seja, não têm partes fracionárias ou decimais, sendo apenas números completos como 0, 1, 2, 3, e assim por diante.
As operações de adição e multiplicação têm uma propriedade especial entre os números naturais chamada de fechamento. Isso significa que, ao somar ou multiplicar dois números naturais, o resultado será sempre outro número natural.
No entanto, a subtração e a divisão entre dois números naturais nem sempre resultam em um número natural. Por exemplo, resulta em
(um número inteiro, mas não natural), e
resulta em uma fração, que também não é um número natural.
Conjunto dos números inteiros (ℤ)
O conjunto dos números inteiros (ℤ) é uma extensão do conjunto dos números naturais que inclui todos os números inteiros positivos, os números inteiros negativos e o zero.
Representado pela letra ℤ (do alemão Zahlen, que significa "números"), esse conjunto abrange tanto números positivos quanto negativos, formando uma linha infinita de números inteiros para ambos os lados do zero.
O conjunto dos números inteiros é composto por números completos, sem partes decimais ou fracionárias, ou seja, todos os números inteiros são valores absolutos. Há fechamento para as operações de adição, subtração e multiplicação, ou seja, o resultado dessas operações entre números inteiros será sempre outro número inteiro.
No entanto, a divisão entre números inteiros nem sempre resulta em um número inteiro. Por exemplo, , que não pertence ao conjunto dos inteiros.
O zero é o elemento neutro da adição no conjunto dos inteiros, pois, ao somar zero a qualquer número inteiro, o valor inicial permanece inalterado. O zero também age como o ponto central desse conjunto, separando os valores positivos dos negativos.
Conjunto de números racionais (ℚ)
O conjunto dos números racionais (ℚ) é formado por todos os números que podem ser escritos como uma fração, na forma , onde
e
são números inteiros e
. Esse conjunto é representado pela letra ℚ (de "quociente") e inclui, portanto, tanto números inteiros quanto frações e números decimais finitos ou infinitos periódicos. Exemplos de números racionais incluem
Uma das características dos números racionais é que eles abrangem uma gama maior de valores que os números inteiros, permitindo representar quantidades que não são inteiras, como partes de um todo ou divisões exatas. Eles incluem os números inteiros, já que qualquer número inteiro pode ser escrito como uma fração (por exemplo, ).
O conjunto dos números racionais é fechado para as operações de adição, subtração, multiplicação e divisão (exceto divisão por zero). Ao realizar qualquer uma dessas operações entre dois números racionais, o resultado será outro número racional. Por exemplo, somando e
, obtemos
, que é um número racional. Assim, os números racionais são úteis para expressar divisões exatas e relações proporcionais.
Os números racionais são muito usados em situações cotidianas, como medir comprimentos, representar notas decimais e descrever divisões precisas entre elementos. Eles formam uma base importante para os números reais, dos quais fazem parte junto com os números irracionais.
O conjunto dos números racionais permite que as operações e representações matemáticas se expandam para além dos valores inteiros, abordando assim uma variedade mais ampla de situações práticas e teóricas.
Conjunto de números irracionais (I)
O conjunto dos números irracionais é formado por todos os números que não podem ser expressos como uma fração da forma , onde
e
são números inteiros e
. Ou seja, os números irracionais não têm uma representação exata como quociente entre dois inteiros.
Em outras palavras, esses números apresentam uma representação decimal infinita e não periódica, ou seja, suas casas decimais se estendem para sempre sem formar um padrão repetitivo. Esse conjunto é geralmente representado pela letra I.
Os números irracionais incluem valores como e
(a base do logaritmo natural). Um exemplo clássico é
que possui uma representação decimal infinita, aproximadamente
, e não apresenta um padrão regular nas suas casas decimais.
Da mesma forma, , que representa a razão entre a circunferência e o diâmetro de um círculo, também é irracional, com um valor decimal (
) que se estende infinitamente sem periodicidade. Esses exemplos ilustram a característica que define os números irracionais: sua impossibilidade de serem expressos como frações exatas entre dois inteiros.
Os números irracionais possuem algumas propriedades únicas. Uma de suas características é a representação decimal infinita e não periódica, o que os distingue dos números racionais, que possuem uma representação decimal finita ou periódica. Os irracionais também não podem ser exatamente escritos na forma . Embora possam ser aproximados por frações, como
, essas frações não representam o valor exato do número irracional, sendo apenas aproximações úteis em cálculos práticos.
Em termos de aplicação, os números irracionais são fundamentais em diversas áreas da matemática e das ciências. Por exemplo, raízes quadradas não exatas, como e
, são irracionais e surgem em cálculos geométricos e trigonométricos. Constantes matemáticas como
e
são essenciais em cálculos de áreas de círculos, crescimento exponencial e em muitas fórmulas da física e da engenharia.
Esses números possibilitam que matemáticos e cientistas realizem cálculos e descrições de fenômenos que não podem ser precisamente representados com frações, mostrando-se indispensáveis na compreensão do mundo físico e na construção de teorias matemáticas.
Conjunto dos números reais (ℝ)
O conjunto dos números reais (ℝ) é formado pela união dos números racionais e dos números irracionais, abrangendo todos os tipos de números que podem ser representados em uma linha numérica contínua. Isto é, os números reais incluem todos os números que podem ser expressos de forma decimal, sejam finitos, infinitos periódicos (racionais) ou infinitos não periódicos (irracionais).
Os números reais podem ser divididos em dois grandes subconjuntos: os números racionais e os irracionais. Uma característica importante desses números é que eles preenchem a reta numérica de maneira contínua. Ou seja, entre dois números reais quaisquer, sempre existe um número real intermediário, o que define a densidade desse conjunto.
Graças a essa propriedade, o conjunto dos números reais é utilizado em cálculos de medidas, distâncias, áreas e em outras representações matemáticas que exigem valores contínuos. A utilização dos números reais é importante para a análise matemática, cálculo e muitas áreas da física e engenharia, onde se trabalha com intervalos contínuos e grandezas mensuráveis.
O conjunto dos números reais é geralmente representado pela letra ℝ. A representação acima mostra que o conjunto dos reais inclui tanto números racionais (como ) quanto irracionais (como
), formando um conjunto contínuo e completo ao longo da reta numérica.
Conjunto dos números complexos (ℂ)
O conjunto dos números complexos (ℂ) é composto por todos os números que podem ser escritos na forma , onde
e
são números reais e
é a unidade imaginária, definida como
. Essa notação permite que os números complexos representem tanto números reais (quando
), quanto números puramente imaginários (quando
), e combinações entre eles.
A existência dos números complexos expande o sistema numérico para incluir soluções de equações que não têm solução no conjunto dos números reais, como a raiz quadrada de números negativos. Os números complexos são divididos em duas partes: a parte real e a parte imaginária
.
O termo "imaginário" surgiu inicialmente por se tratar de uma extensão abstrata dos números reais, mas, na prática, os números complexos têm aplicações importantes em áreas como física, engenharia elétrica e análise matemática. Por exemplo, circuitos elétricos e ondas são modelados usando números complexos, pois eles permitem representar tanto a magnitude quanto a fase de um sinal.
Uma propriedade essencial dos números complexos é que eles formam um sistema fechado para as operações de adição, subtração, multiplicação e divisão (exceto divisão por zero). Isto é,qualquer operação entre números complexos resulta em outro número complexo, possibilitando cálculos completos dentro desse conjunto.
Esse fechamento torna os números complexos uma ferramenta poderosa para resolver equações e problemas que não podem ser abordados apenas com números reais. O conjunto dos números complexos é representado pela letra ℂ e inclui todos os números reais e imaginários.
Essa representação mostra que o conjunto dos números complexos inclui números puramente reais (como ) e números com partes imaginárias (como
e
), formando um conjunto abrangente que estende o conceito de número para além da reta numérica, representando-os em um plano bidimensional.
Intervalos numéricos
O intervalo na matemática é um conjunto de números reais que estão entre dois valores específicos, chamados de limites. Intervalos são representados usando colchetes e parênteses para indicar quais limites estão incluídos ou excluídos. Eles são uma maneira prática de definir uma faixa contínua de números em que todos os valores entre os limites são parte do conjunto.
-
Intervalo fechado
- neste intervalo, ambos os limites
e
estão incluídos no conjunto. A notação com colchetes indica essa inclusão. Por exemplo, o intervalo
inclui todos os números entre
e
, incluindo os próprios
e
.
-
Intervalo aberto
- os limites
e
não fazem parte do conjunto, mas todos os números entre eles estão incluídos. Esse intervalo é indicado por parênteses. Por exemplo,
inclui todos os números entre
e
, mas exclui os próprios valores
e
.
-
Intervalo semiaberto ou semifechado
ou
- esse tipo de intervalo inclui apenas um dos limites. A notação
indica que o limite inferior
está incluído, mas o superior
não está. Por outro lado,
inclui
, mas não
. Por exemplo,
, inclui o número
mas não
, enquanto
inclui
, mas não
.
-
Intervalo infinito - usado para descrever conjuntos que não têm um limite superior ou inferior. Um intervalo pode se estender até o infinito, como
, que representa todos os números reais menores ou iguais a
. Da mesma forma,
representa todos os números reais maiores ou iguais a
.
Intervalos são amplamente utilizados na matemática e na física, especialmente em cálculo e análise. Eles permitem definir domínios de funções, delimitar o escopo de integrações e indicar as soluções de desigualdades.
Os intervalos também são uma ferramenta para indicar a faixa de valores onde uma variável pode atuar, tornando-os indispensáveis em áreas que envolvem limites numéricos.
Relação entre os conjuntos numéricos
Os conjuntos numéricos formam uma hierarquia, onde cada conjunto engloba o anterior. Iniciando pelos naturais e passando pelos inteiros e racionais que, junto aos irracionais, determinam os reais. Por sua vez, o conjunto dos reais está contido no conjunto dos complexos.
Os números naturais (ℕ) são os números que usamos para contar: . Eles são a base de todos os conjuntos numéricos e representam os valores não negativos.
O conjunto dos números inteiros (ℤ) inclui todos os números naturais, seus opostos negativos e o zero. Ele expande os números naturais ao incluir os negativos:
Os números racionais (ℚ) abrangem todos os valores que podem ser expressos como uma fração de dois inteiros, com
. Incluem frações e decimais periódicos, formando um conjunto que cobre valores entre os inteiros.
Os números irracionais são aqueles que não podem ser representados como frações de inteiros, como e
. Esses números possuem uma expansão decimal infinita e não periódica, representando valores que completam os números reais sem repetir ou formar padrões.
Os números reais (ℝ) combinam todos os números racionais e irracionais, abrangendo toda a linha numérica. Finalmente, os números complexos (ℂ) incluem todos os números reais e os números imaginários, como .
Eles são escritos na forma , onde
e
são reais, permitindo resolver equações que os números reais não podem resolver, especialmente aquelas envolvendo raízes de números negativos.
Veja também: