Exercícios sobre Teorema de Tales para estudar (com gabarito explicado)
O Teorema de Tales é utilizado no estudo se segmentos proporcionais, determinados por retas paralelas cruzadas por transversais.
Estes exercícios vão te ajudar a compreender melhor este importante teorema da Geometria.
Exercício 1
Na figura abaixo, as retas r, s e t são paralelas e cortadas por duas retas transversais, u e v. Determine a medida do segmento x.
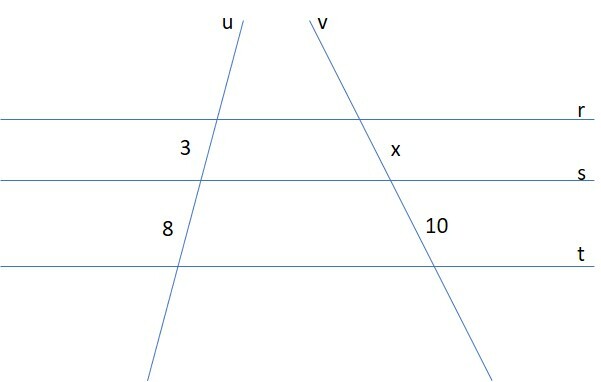
A) 1
B) 3,75
C) 4,25
D) 9
E) 18
Pelo Teorema de Tales, quando um feixe de retas paralelas é cortado por duas transversais, os segmentos determinados sobre as transversais são proporcionais.
Neste caso, temos a proporção:
3/8 = x/10
Utilizando a propriedade fundamental das proporções:
8 × x = 3 × 10
Resolvendo:
8x = 30
x = 30/8
x = 3,75
Resposta correta: B) 3,75 cm
Exercício 2
Na figura abaixo, as retas r, s e t são paralelas. Determine os valores de x e y, sabendo que x + y = 12 cm.
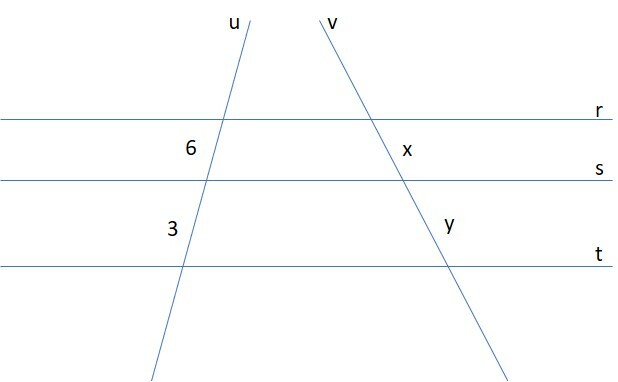
a) x = 8 cm e y = 12 cm
b) x = 8 cm e y = 4 cm
c) x = 10 cm e y = 12 cm
d) x = 11cm e y = 16 cm
e) x = 12 cm e y = 8 cm
Resolução:
Pelo Teorema de Tales, os segmentos formados pelas retas paralelas em duas transversais são proporcionais. Portanto, podemos escrever a seguinte proporção:
Logo, para y:
x + y = 12
y = 12 - x
y = 12 - 8
y = 4 cm
Exercício 3
Na figura abaixo, as retas r, s e t são paralelas. Se AB = 15 cm, BC = 10 cm e DE = 9 cm, qual é o valor de EF
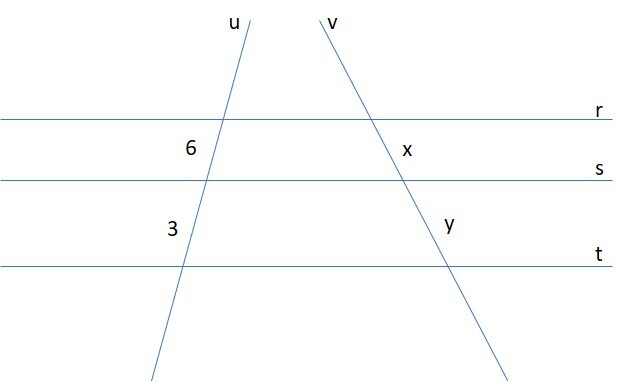
A) 4 cm
B) 5 cm
C) 6 cm
D) 7 cm
E) 8 cm
Pelo Teorema de Tales, quando um feixe de retas paralelas é cortado por duas transversais, os segmentos determinados sobre as transversais são proporcionais.
Podemos estabelecer a proporção:
AB/BC = DE/EF
Substituindo os valores conhecidos:
15/10 = 9/DE
Multiplicando os meios pelos extremos:
15 × DE = 10 × 9
Resolvendo:
15DE = 90
DE = 90/15
DE = 6
Verificando as alternativas: A alternativa correta é a C) 6 cm
Resposta correta: C) 6 cm
Exercício 4
Na figura abaixo, as retas r, s, t e u são paralelas e cortadas por duas transversais. Todas as medidas estão em centímetro. É sabido que A + B + C = 36 cm. Determine as medidas de A, B e C.
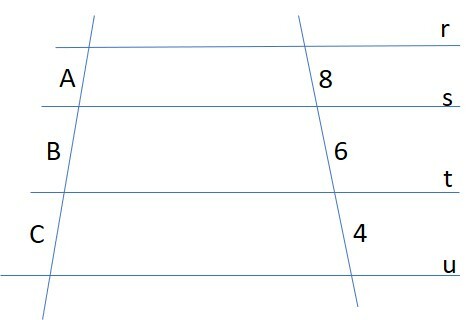
a) A = 2 cm, B = 8 cm e C = 6 cm
b) A = 4 cm, B = 9 cm e C = 3 cm
c) A = 9 cm, B = 10 cm e C = 6 cm
d) A = 8 cm, B = 12 cm e C = 16 cm
e) A = 6 cm, B = 10 cm e C = 6 cm
Para resolver este problema, vamos utilizar o Teorema de Tales, que afirma que quando retas paralelas são cortadas por retas transversais, os segmentos formados são proporcionais.
Para a primeira proporção, tomemos a medida fornecida na chave, 36 cm, em razão com o segmento A.
A outra razão será o segmento correspondente 4 com o total 8 + 6 + 4.
Para a segunda proporção:
Para a terceira proporção:
Logo, a reposta é:
A = 8 cm, B = 12 cm e C = 16 cm
Quer continuar fazendo exercícios sobre o Teorema de Tales? Então experimente o Toda Matéria Plus!
Você pode querer conhecer mais sobre outro importante teorema da Matemática, o Teorema de Pitágoras.
-
Teorema de Pitágoras
-
Fórmula de Bhaskara: o que é e como se calcula

-
Exercícios sobre equação do 2º grau (com gabarito resolvido)

-
Exercícios sobre fórmula de Bhaskara para praticar (com gabarito)

-
Exercícios sobre polígonos para treinar (com respostas explicadas)

-
Exercícios sobre Teorema de Pitágoras (com gabarito resolvido)

-
Exercícios sobre ângulos (com gabarito resolvido e explicado)

-
Exercícios sobre MMC e MDC (com questões explicadas)

-
Exercícios sobre potenciação para praticar (com respostas explicadas)

-
Exercícios de matemática básica para estudar (com respostas explicadas)

