Números racionais
Os números racionais são aqueles que podem ser expressos como frações, ou seja, como o quociente de dois números inteiros. Em termos matemáticos, um número racional é qualquer número que pode ser representado na forma onde
e
são números inteiros, e
O número é chamado de numerador, enquanto o número
é chamado de denominador. Esses números englobam tanto as frações propriamente ditas quanto os números inteiros, já que qualquer número inteiro pode ser expresso como uma fração com denominador 1.
Além disso, os números decimais finitos ou periódicos também são racionais, uma vez que são convertíveis em frações. Exemplos de números racionais:
-
é um número racional, uma fração com numerador 3 e denominador 4.
-
também um número racional, pois é a fração que representa o quociente de -5 e 2.
-
é um número inteiro, que pode ser escrito como
e, portanto, é racional.
-
é um número decimal finito que é racional, pois pode ser expresso como
-
é um número decimal periódico, que pode ser representado como
Conjunto dos números racionais
O conjunto dos números racionais é representado pela letra , que vem da palavra latina quotient, que significa "quociente". O conjunto
inclui todos os números que podem ser expressos na forma
onde
e
são inteiros e
Além dos números inteiros, o conjunto dos números racionais inclui frações simples, números decimais finitos e periódicos.
Operações com números racionais
Adição e subtração de números racionais
Para somar ou subtrair números racionais, é necessário ter o mesmo denominador. Depois, realizamos a soma ou a subtração dos numeradores e o denominador permanece o mesmo.
Exemplo de soma:
Exemplo de subtração:
Exemplo com denominadores diferentes
Com números racionais que têm denominadores diferentes, precisamos realizar um passo intermediário antes de somar ou subtrair: igualar os denominadores. Para isso, encontramos um denominador comum, que geralmente é o mínimo múltiplo comum (MMC) dos denominadores.
No exemplo de soma abaixo, seguimos os passos:
- Fazer o MMC dos denominadores 3 e 4. MMC (3, 4) = 12.
- Ajustar as frações para ter o denominador 12. Para
multiplica-se numerador e denominador por 4, obtendo
Para
multiplica-se numerador e denominador por 3, obtendo
- Realizar a soma, agora que os denominadores são iguais.
No exemplo de subtração abaixo, seguimos os mesmos passos:
- Fazer o MMC dos denominadores 10 e 5. MMC (10, 5) = 10.
- Ajustar as frações para ter o denominador 10.
já tem o denominador necessário. Para
multiplica-se numerador e denominador por 2, obtendo
- Subtrair os numeradores:
Multiplicação de números racionais
A multiplicação de frações é feita multiplicando-se diretamente os numeradores entre si e os denominadores entre si. Exemplo:
Divisão de números racionais
Para dividir frações, multiplicamos a primeira fração pelo inverso da segunda. O inverso de uma fração é
Exemplo:
Potenciação
Quando se trata de potência de frações, aplicamos a potência a cada parte da fração separadamente. Ou seja, elevamos o numerador e o denominador à potência desejada. Exemplo:
Simplificação
Para simplificar uma fração, dividimos o numerador e o denominador pelo maior divisor comum (MDC) entre eles. O objetivo é reduzir a fração a uma forma mais simples e fácil de entender. Exemplo:
Em exercícios, muitas vezes a resposta correta de uma operação matemática é uma fração em sua forma simplificada. Por isso, é importante estar atento.
Exercícios com números racionais
Exercício 1
Quais dos números abaixo são números racionais?
a)
b)
c)
d)
Exercício 2
Resolva a operação:
a)
b)
c)
Exercício 3
Resolva a operação matemática:
a)
b)
c)
d)
Exercício 4
Considere os números racionais: e
- Verifique se
- Verifique se
a)
b)
c)
d)
Veja também
Você pode querer praticar:
-
Atividades de Português para o 5º ano (para praticar)

-
Tabuada completa de multiplicação, adição, divisão e subtração

-
Atividades de Português para o 6º ano (com folhas para imprimir)

-
Exercícios sobre pronomes para praticar (com respostas)

-
Exercícios sobre números racionais (questões resolvidas)

-
Número

-
MMC e MDC
-
Raiz quadrada (√)
-
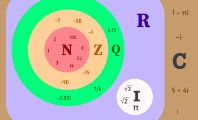
Conjuntos numéricos
-
Exercícios sobre MMC e MDC (com questões explicadas)


