Polígonos
Um polígono é uma figura geométrica plana e fechada formada por segmentos de retas, chamados de lados. Conforme a quantidade de lados que as formam, estas figuras possuem nomes e formatos diferentes.
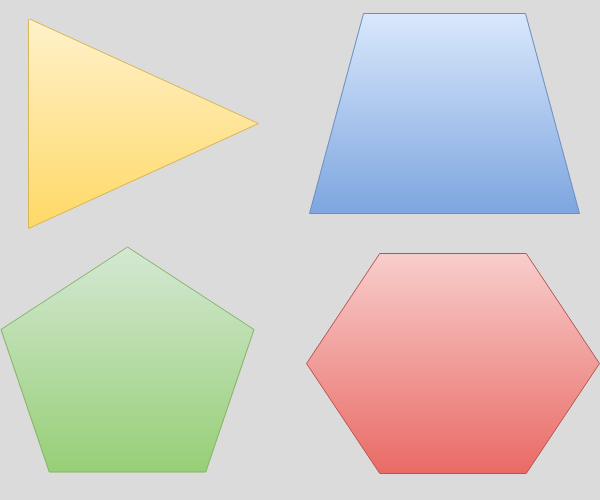Polígonos formados por 3 (triângulo), 4 (quadrilátero), 5 (pentágono) e 6 (hexágono) segmentos de reta
Para uma figura ser um polígono a linha poligonal que a forma não pode deixar partes em aberto, ainda, não pode haver partes arredondadas.
O estudo dos polígonos pertence à área da Matemática chamada geometria.
Nomes e tipos dos polígonos
Os polígonos são classificados segundo o número de lados que os formam, recebendo um nome diferente para cada formato. Não existem polígonos formados por apenas um ou dois segmentos de reta. A partir de três segmentos, estas figuras geométricas já são formadas.
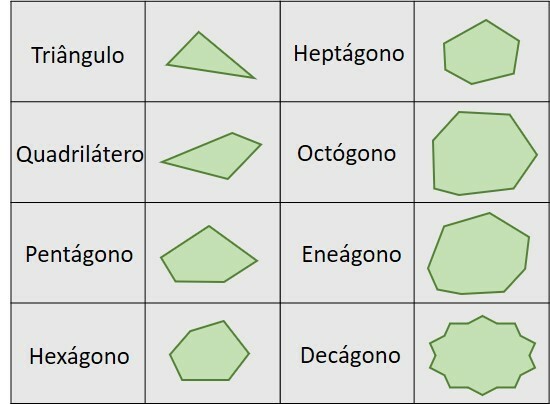
Veja os nomes dos diferentes tipos de polígonos, conforme a quantidade de lados que possuem.
| Nº de lados | Nome | Nº de lados | Nome |
|---|---|---|---|
| 3 | Triângulo | 16 | Hexadecágono |
| 4 | Quadrilátero | 17 | Heptadecágono |
| 5 | Pentágono | 18 | Octodecágono |
| 6 | Hexágono | 19 | Eneadecágono |
| 7 | Heptágono | 20 | Icoságono |
| 8 | Octógono | 30 | Triacontágono |
| 9 | Eneágono | 40 | Tetracontágono |
| 10 | Decágono | 50 | Pentacontágono |
| 11 | Undecágono | 60 | Hexacontágono |
| 12 | Dodecágono | 70 | Heptacontágono |
| 13 | Tridecágono | 80 | Octacontágono |
| 14 | Tetradecágono | 90 | Eneacontágono |
| 15 | Pentadecágono | 100 | Hectágono |
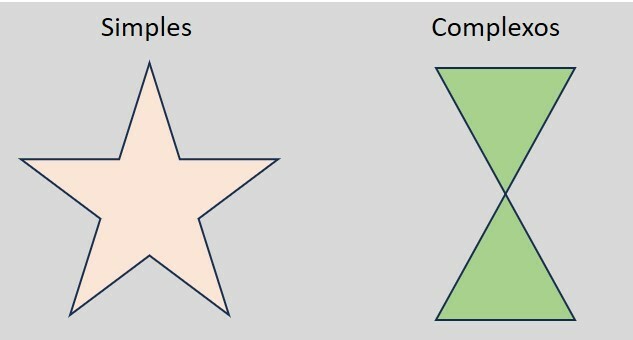
Polígonos simples e complexos
Outra característica que classifica os polígonos é a existência ou não de cruzamentos de seus lados. Os polígonos onde não há cruzamento são chamados de simples, enquanto os que possuem ao menos um cruzamento são os complexos.
Elementos de um polígono
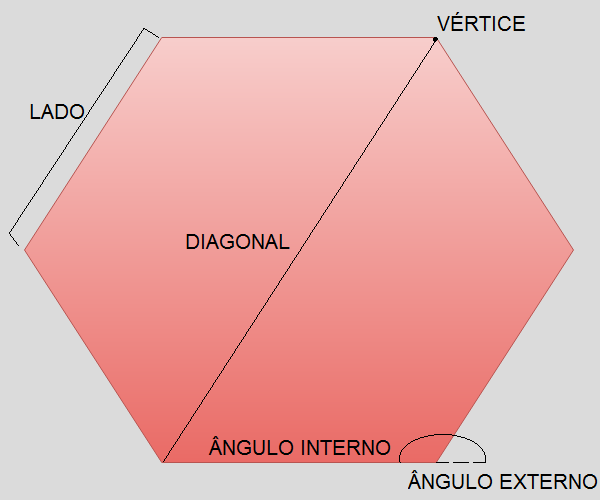
Além dos lados que dão forma aos polígonos, eles possuem outros elementos que são: os vértices, as diagonais e os ângulos (internos e externos).
Os lados são todos os segmentos de reta que formam o polígono. Os vértices são os pontos de encontro dos segmentos de retas e as diagonais são segmentos de reta que fazem a ligação de dois vértices não adjacentes.
Os ângulos internos são os ângulos formados por dois lados consecutivos do polígono, localizados em seu interior. Já os ângulos externos são formados por um lado da figura juntamente como o prolongamento do lado adjacente.
Partes de um polígono
Polígonos regulares e irregulares
Os polígonos serão regulares quando:
- todos os seus lados tiverem a mesma medida;
- todos os seus ângulos internos forem congruentes, isto é, possuírem a mesma medida;
- forem inscritíveis em um círculo, ou seja, quando todos os seus vértices forem pontos de uma mesma circunferência.
Em contrapartida, serão irregulares quando não apresentarem tais características.
Perímetro dos polígonos
O perímetro de qualquer forma fechada é a medida de seu contorno. Isso significa que o perímetro é um comprimento podendo ser medido, por exemplo, em metros, centímetros ou quilômetros.
Nos polígonos, cálculo do perímetro é a soma da medida de todos seus lados.
No caso particular do polígono ser regular, como todos seus lados são iguais, basta multiplicar a medida de um lado pela quantidade de lados.
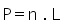
Área dos polígonos
Área é a medida de uma superfície e, como os polígonos são figuras planas, o estudo do cálculo de suas áreas é fundamental na geometria.
O cálculo para os polígonos seguem regras algébricas, com fórmulas próprias a depender do número de lados. Chamando a área dos polígonos de A, confira as fórmulas para alguns a seguir.
Área do triângulo
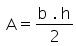
Área do quadrado
Área do retângulo
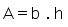
Área do trapézio
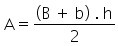
Área do losango
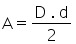
Área dos polígonos regulares
Quando os polígonos forem regulares, a área pode ser calculada pelo produto entre o perímetro e o apótema e o resultado, dividido por dois.
Apótema e o seguimento que liga o ponto central do polígono ao meio de qualquer de seus lados.
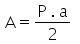
Número de diagonais
Diagonal é um seguimento interno ao polígono que liga dois vértices não consecutivos.
O número de diagonais em um polígono pode ser determinado pela seguinte fórmula:
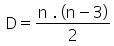
Ângulos nos polígonos
O encontro de dois lados de um polígono determina um ângulo, sendo a medida da abertura entre estes. Esta medida é feita comumente em graus.
Soma dos ângulos internos
Para determinar a soma dos ângulos internos em polígonos regulares, utiliza-se a fórmula:
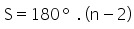
Soma dos ângulos externos
Independente do número de lados de um polígono, a soma dos ângulos externos é sempre igual a 360º.
Classificação em convexo e não convexo
Para descobrir se um polígono é convexo ou não convexo é preciso traçar uma reta entre dois pontos pertencentes a ele.
Polígono convexo
Um polígono será classificado como convexo quando todas as retas traçadas ficarem na área do polígono.
Se a medida de todos os ângulos internos do polígono for menor que 180º, então ele será convexo.
Polígono côncavo
Para um polígono ser classificado como côncavo (ou não convexo) basta que apenas uma das retas traçadas atravesse algum ponto que esteja fora da área do polígono.
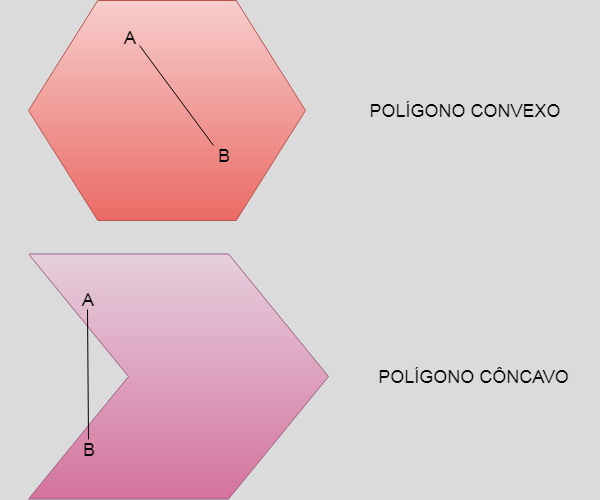Polígono convexo e polígono côncavo
Veja também:
