Raiz quadrada (√)
A raiz quadrada é um número que corresponde a multiplicação de dois números iguais, isso quer dizer, quando multiplicamos um número por ele mesmo.
Por exemplo, quando multiplicamos o número 5 por ele mesmo: 5 x 5 = 25. Logo, a raiz quadrada de 25 é 5. O símbolo da raiz quadrada é √.
Existem as raízes quadradas exatas, quando o resultado de uma raiz quadrada é um número inteiro (é o caso da √25=5), e raízes quadradas não exatas, quando o resultado de uma raiz quadrada é um número racional decimal "quebrado".
Há uma nomenclatura específica para cada um dos elementos que compõem a raiz quadrada, conheça quais são os nomes:
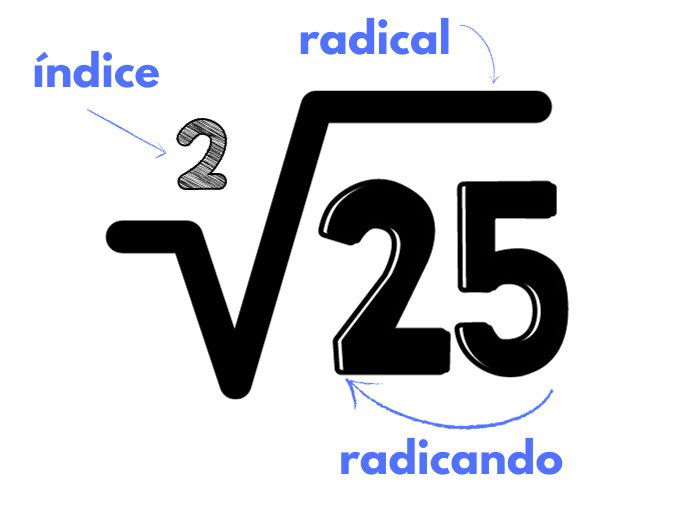
Note que o radical é símbolo da raiz quadrada, o radicando é número que calcularemos a raiz quadrada, já o índice é o indicador de que se trata de uma raiz quadrada. Caso o índice fosse o número 3, seria uma raiz cúbica. A resposta desta operação chama-se raiz quadrada.
Entretanto, normalmente, quando o índice é 2, suprime-se o número. Por isso, quando o espaço referente ao índice estiver em branco, sabe-se que é uma raiz quadrada.
Como fazer a raiz quadrada
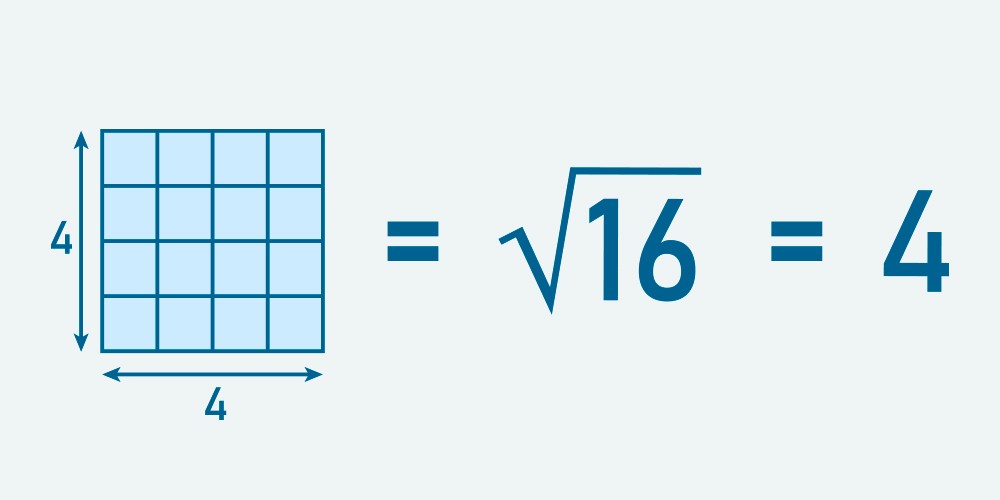
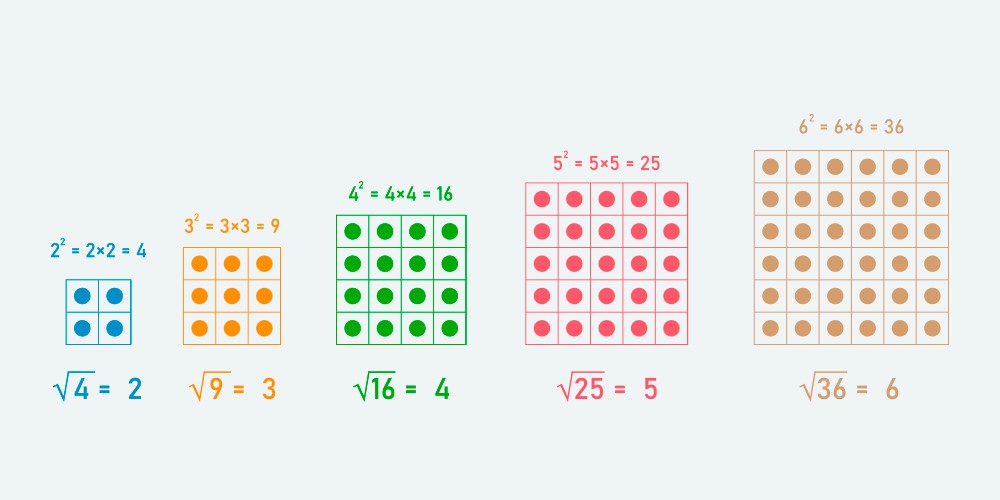
Para calcular uma raiz quadrada exata, basta conhecermos o número que, quando multiplicado por ele mesmo, tem como resultado o radicando.
Conhecer a tabuada pode ajudar bastante a saber a raiz quadrada de números menores. Como no exemplo acima, ao saber que 4 x 4 = 16, entende-se que a √ 16 = 4.
Quando a raiz quadrada tem como resultado um número inteiro, como no exemplo, chama-se raiz quadrada exata, mas quando o resultado da raiz quadrada de um número não é inteiro, nomeia-se de raiz quadrada não exata. Saiba como calcular nos dois casos:
Calcular raiz quadrada exata
Ao saber a tabuada, o cálculo do valor de algumas raízes quadradas será simples. Porém, em casos em que não se conhece a tabuada ou em número mais elevados, pode descobrir a raiz quadrada usando a fatoração. Veja o mesmo exemplo anterior, mas feito com o auxílio da fatoração:
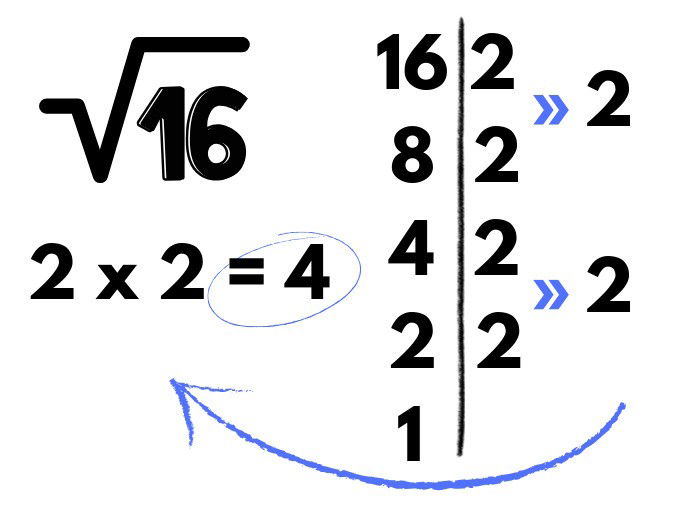
Para calcular a raiz quadrada, fatoramos o número 16. Após a fatoração, observamos os números pelos quais 16 foi fatorado, vemos que foi dividido quatro vezes pelo número 2.
Por ser uma raiz quadrada, a cada dois números iguais, destacamo-los. Destacamos o número dois duas vezes. Em seguida, faz-se a multiplicação dos números destacados: 2 x 2 = 4, logo a √ 16 = 4.
Calcular raiz quadrada não exata
A raiz quadrada não exata é aquela que o seu resultado não será um número inteiro. Nesses casos, a tabuada não ajuda muito, sendo a fatoração a forma mais eficaz de alcançar o resultado.
Por exemplo: quanto é √ 20? Sabemos que não existe um número inteiro que multiplicado por ele mesmo tenha como resultado o número 20. Entenda como fazer o cálculo nesses casos:
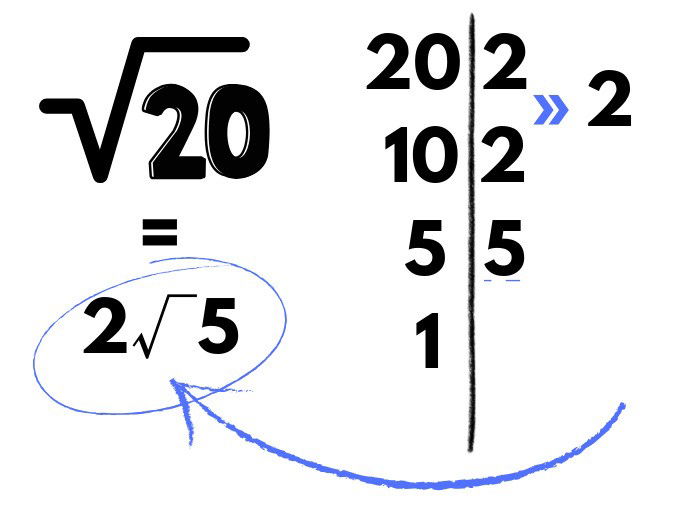
Ao fazermos a fatoração, vemos que dos números pelos quais 20 foi fatorado, temos o 2 e o 5. Por ser uma raiz quadrada, destacamos o número 2, que apareceu duas vezes, ficando fora da raiz quadrada. Já o número 5, que apareceu somente uma vez, permanece no radical. A resposta é 2√5.
Calcular raiz quadrada aproximada
Há ainda outro tipo de cálculo de raiz quadrada para alcançar um resultado aproximado. Esse tipo de cálculo é usado para números que não tem raiz quadrada exata (e quando a fatoração não é uma opção).
Por exemplo, qual seria a √ 5? Veja o cálculo:
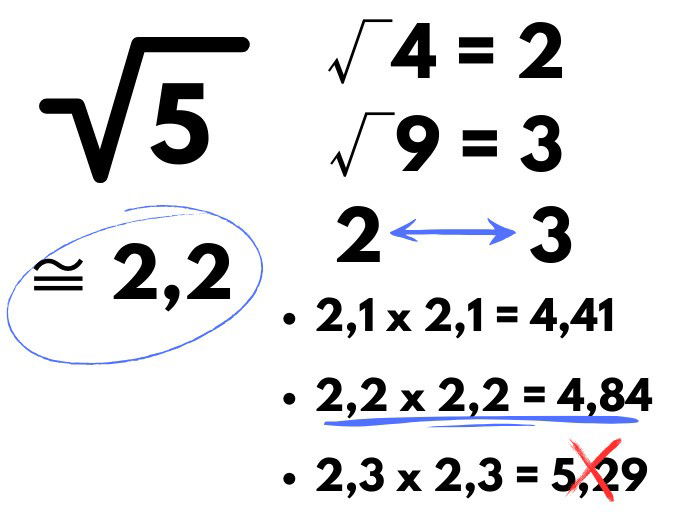
No caso da raiz quadrada de 5, sabemos que não há nenhum número exato que multiplicado por ele mesmo o resultado seja 5. Porém, conhecemos os números próximos ao 5 que tem a raiz quadrada exata, 4 e 9, sendo √4 = 2 e √ 9 = 3.
Conhecendo o resultado dessas raízes quadradas, percebemos que a raiz quadrada de 5 está entre 2 e 3. Assim, por tentativa e erro, multiplicados os números: 2,1, 2,2 e 2,3 por eles mesmos. O resultado mais próximo de 5 foi o de 2,2. Por isso, √5 ≅ 2,2.
Veja também a tabuada de multiplicação.
Tabuada da raiz quadrada
Conheça os resultados de algumas raízes quadradas exatas:
| √ 0 = 0 | √ 729 = 27 |
| √ 1 = 1 | √ 784 = 28 |
| √ 4 = 2 | √ 841 = 29 |
| √ 9 = 3 | √ 900 = 30 |
| √ 16 = 4 | √ 961 = 31 |
| √ 25 = 5 | √ 1024 = 32 |
| √ 36 = 6 | √ 1089 = 33 |
| √ 49 = 7 | √ 1156 = 34 |
| √ 64 = 8 | √ 1225 = 35 |
| √ 81 = 9 | √ 1296 = 36 |
| √ 100 = 10 | √ 1369 = 37 |
| √ 121 = 11 | √ 1444 = 38 |
| √ 144 = 12 | √ 1521 = 39 |
| √ 169 = 13 | √ 1600 = 40 |
| √ 196 = 14 | √ 1681 = 41 |
| √ 225 = 15 | √ 1764 = 42 |
| √ 256 = 16 | √ 1849 = 43 |
| √ 289 = 17 | √ 1936 = 44 |
| √ 324 = 18 | √ 2025 = 45 |
| √ 361 = 19 | √ 2116 = 46 |
| √ 400 = 20 | √ 2209 = 47 |
| √ 441 = 21 | √ 2304 = 48 |
| √ 484 = 22 | √ 2401 = 49 |
| √ 529 = 23 | √ 2500 = 50 |
| √ 576 = 24 | √ 2601 = 51 |
| √ 625 = 25 | √ 2704 = 52 |
| √ 676 = 26 | √ 2809 = 53 |
Exemplos de exercícios com raiz quadrada
Exercício 1
Uma empresa de jardinagem está construindo um jardim quadrado em um quintal. A área total do jardim é 81 metros quadrados. Qual é o comprimento do lado do jardim?

Resposta: O comprimento é de 9 metros.
Exercício 2
Júlia está planejando um painel quadrado para sua sala. A área total do painel é 144 metros quadrados. Qual é a medida do lado do painel?
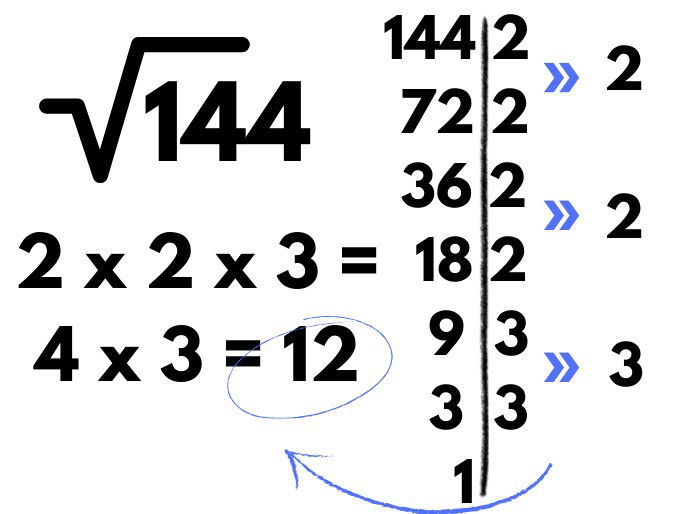
Resposta: A medida do lado do painel é de 12 metros.
Exercício 3
Um clube tem uma piscina quadrada com área de 180 metros. Qual é o tamanho do lado da piscina?
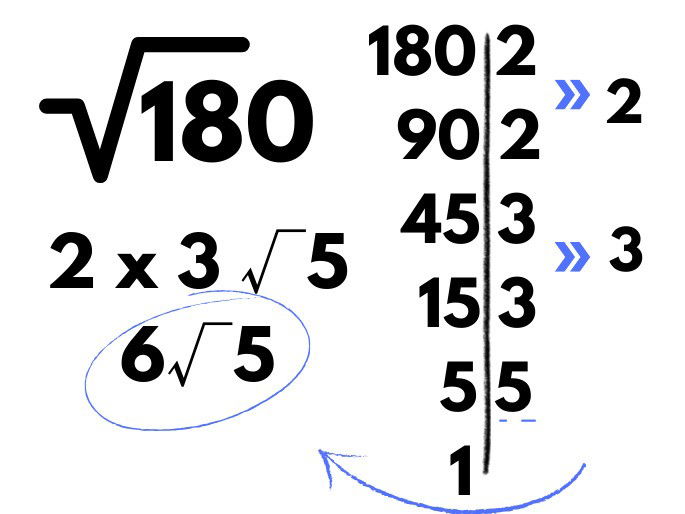
Resposta: O tamanho do lado da piscina é 6√5.
Exercício 4
Um agricultor tem uma horta quadrada com área total de 300 metros. Qual é a largura aproximada da horta?
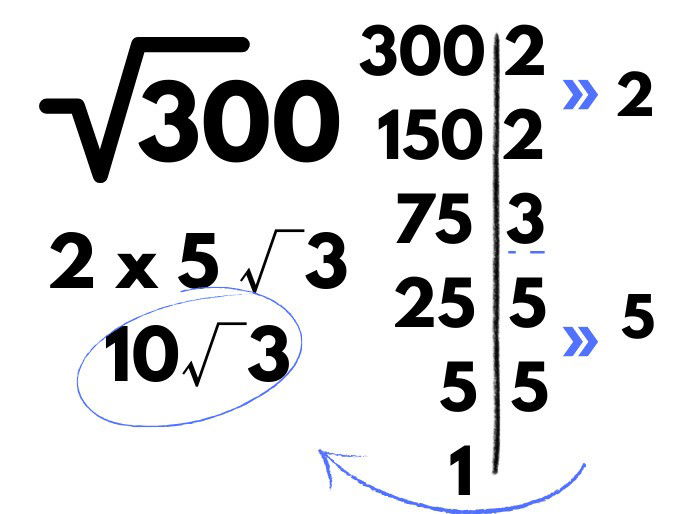
Resposta: A largura é 10√3.
Saiba também como:
- Fazer a regra de 3
- Calcular o Teorema de Pitágoras
- Calcular soma e produto em equações do 2º grau
- Reconhecer os números primos
- Entender os conjuntos numéricos
- Entender o conjunto dos números naturais
-
Atividades das tabuadas de multiplicação (para imprimir)

-
Tabuada Completa de multiplicação, adição, divisão e subtração

-
Folhas de atividades da tabuada de divisão (para imprimir)

- Metro Quadrado (m²): o que é e como calcular
-
Números racionais

-
MMC e MDC
-
Soma e Produto nas Equações do 2ª Grau
-
Exercícios sobre MMC e MDC (com questões explicadas)

-
Fórmula de Bhaskara: o que é e como se calcula

-
Números primos


