Regra de 3
A regra de 3 é uma técnica matemática usada para encontrar um valor desconhecido a partir de proporções. Recebe esse nome porque com base em três valores proporcionais conhecidos, consegue-se calcular um quarto.
Há dois tipos de regra de 3: simples e composta. A regra simples é aplicada quando há apenas duas grandezas envolvidas, já a composta é calculada quando há três grandezas ou mais envolvidas.
A regra de 3 simples e compostas podem ser diretamente proporcionais ou inversamente proporcionais. Na primeira, quando uma grandeza cresce, a outra também aumenta proporcionalmente. Já na segunda, quando uma grandeza cresce, a outra diminui na mesma proporção.
Como fazer a regra de 3
A regra de 3 é usada para calcular e resolver problemas que têm grandezas proporcionais. Ou seja, se há três valores conhecidos que são proporcionais, consegue-se saber um quarto valor desconhecido.
É mais simples entender a regra de 3 por meio de exemplos. Imaginemos que três vestidos em uma loja custam 30 reais, podemos usar a regra de 3 para calcular o valor de 5 vestidos. Estrutura-se o cálculo da seguinte forma:
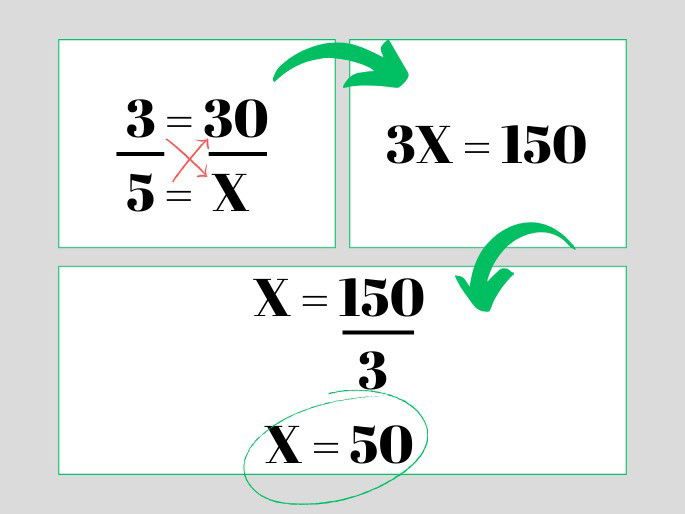
O 3 é o número de vestidos que custam 30 reais, são posicionados um ao lado do outro, após o sinal de igual (=). O 5 fica abaixo do 3, porque é o número de vestidos que se quer saber quanto custa. O valor dos 5 vestidos é desconhecido, que iremos calcular, portanto, é colocado como X.
Trata-se de uma regra de 3 diretamente proporcional, já que o quantos mais vestidos são comprados, maior é o preço. Faz-se então a multiplicação cruzada, multiplicando o 3 com o X e o 5 com 30. Em seguida, divide-se o resultado das multiplicações, chegando ao valor dos 5 vestidos, 50 reais (X=50).
Esse cálculo é uma regra de 3 simples, em que foram usadas duas grandezas, o número de vestidos e o valor deles.
Exemplos de regra de 3
Veja diferentes exemplos de como a regra de 3 pode ser usada.
Regra de 3 diretamente proporcional
É chamada de regra de 3 diretamente proporcional quando uma das grandezas aumenta e a outra grandeza também cresce, na mesma proporção. Vejamos a questão: se em uma loja 4 litros de suco custam R$ 20,00, quanto custará 6 litros?
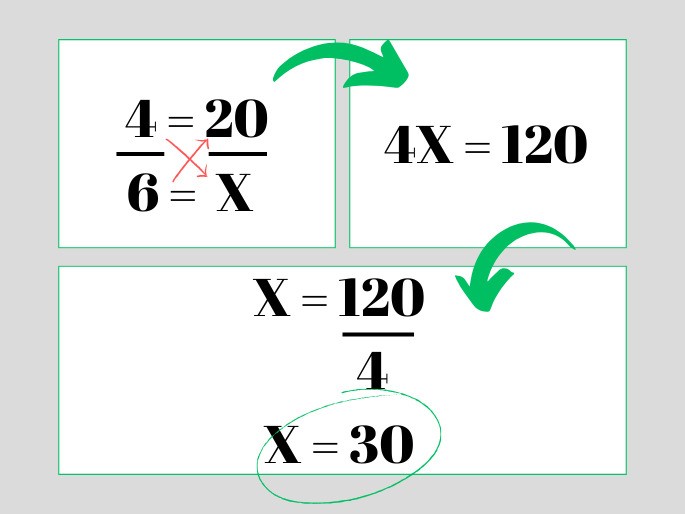
Resposta: 6 litros de suco custarão R$ 30,00.
Regra de 3 inversamente proporcional
Trata-se da regra de 3 inversamente proporcional quando uma das grandezas aumenta, a outra diminui, na mesma proporção. Exemplo: se 5 trabalhadores constroem uma casa em 10 dias, em quantos dias 8 trabalhadores construiriam a mesma casa?
Por ser uma regra de 3 inversamente proporcional, já que quanto maior o número de trabalhadores, em menos tempo as casas serão construídas. Neste caso, é necessário inverter o valor da grandeza inversamente proporcional.
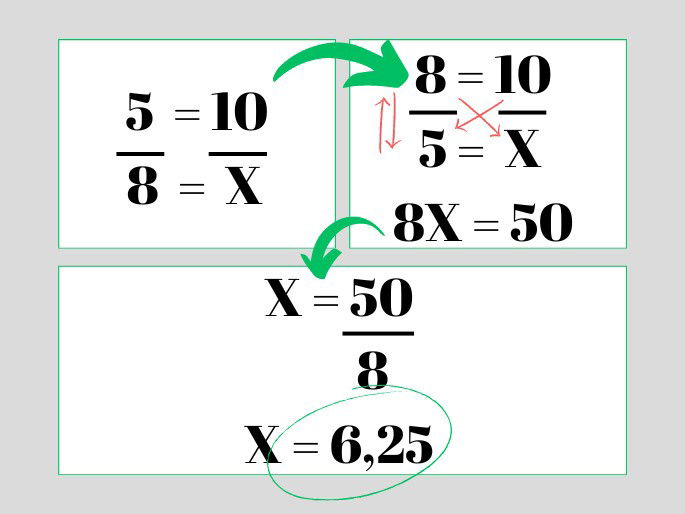
Resposta: os 8 trabalhadores construiriam a casa em 6,25 dias.
Regra de 3 usando porcentagem
A regra de 3 utilizando valores em porcentagem não altera a forma de realizar o cálculo. Por exemplo, na questão: uma loja tem todos os produtos com desconto de 15% durante uma promoção. Se um item originalmente custava R$ 80, quanto pagaria pelo mesmo produto durante a promoção?
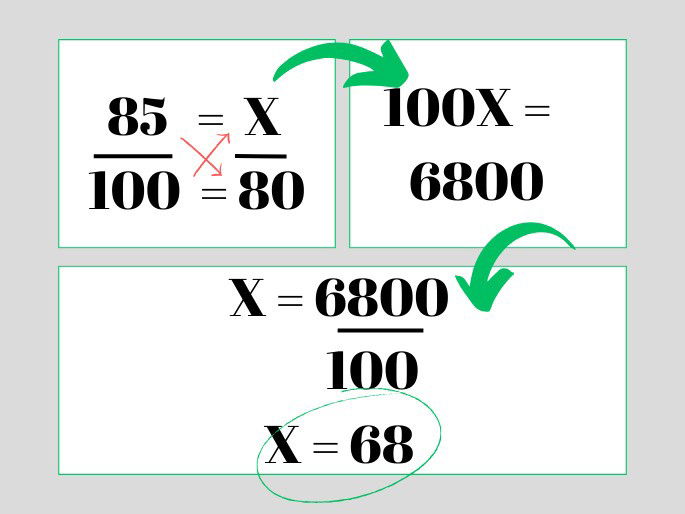
Resposta: durante a promoção, o valor do item seria de R$ 68,00.
Regra de 3 usando unidades distintas
O uso de unidades distintas também não muda a forma de fazer a regra de 3, veja o exemplo com horas e quilômetros: se um carro percorre 240 km em 3 horas, a que velocidade média ele está indo?
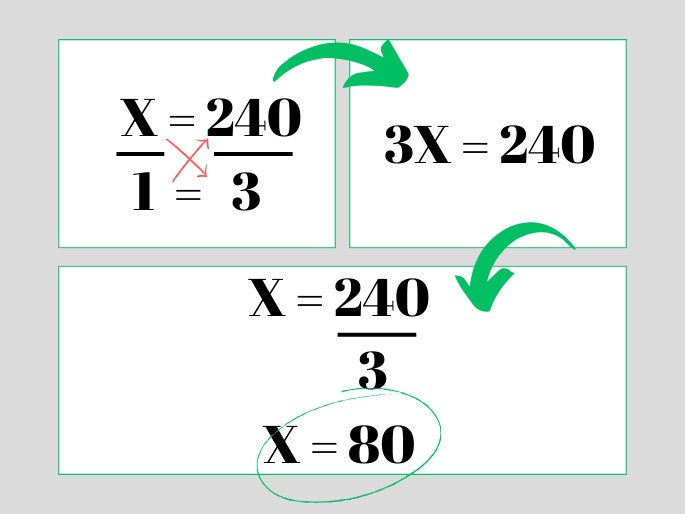
Resposta: a velocidade média é de 80 km/h.
Regra de 3 simples e composta
A diferença entre a regra de 3 simples e composta é que na primeira são adotadas apenas duas grandezas. Na regra de 3 composta, adota-se três ou mais grandezas. Entenda com exemplos:
Regra de 3 simples
Um veículo tem um gasto médio de 15km por litro de combustível. Quantos livros vão ser consumidos para percorrer 300km. Observe que nesse cálculo, usamos duas grandezas: quilômetros e litros.
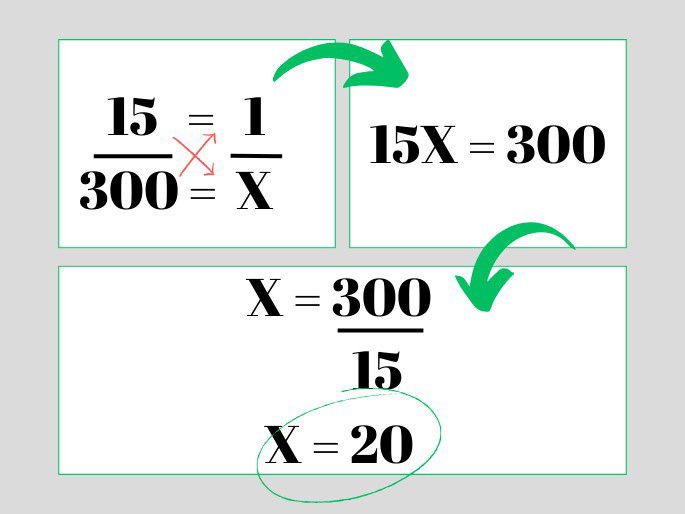
Resposta: serão necessários 20 litros de combustível.
Regra de 3 composta
Na regra de 3 composta, há três grandezas ou mais. Assim como a regra de 3 simples, a regra de 3 composta pode ser diretamente proporcional e inversamente proporcional. É preciso analisar a proporção conforme a questão a ser resolvida.
Veja o exemplo: um condomínio está sendo construído, sabe-se que 5 pedreiros demoram 30 dias para construir 2 casas. Quantos dias 10 pedreiros demorarão para erguer as 6 casas? Observe que estamos trabalhando com três grandezas: número de pedreiros, dias e casas.
Além disso, na regra de 3 composta, temos que observar a relação entre as duas (ou mais) grandezas envolvidas com a grandeza que se quer descobrir.
Neste caso, a grandeza que queremos conhecer é do número de dias. Então, vemos que a relação entre o número de pedreiros e dias é inversamente proporcional, pois conforme o número de pedreiros disponíveis aumenta, os dias para a construção diminuem.
Já a relação entre o número de casas e dias é diretamente proporcional, ou seja, quantos mais dias se têm, mais casas podem ser construídas. Veja o cálculo:
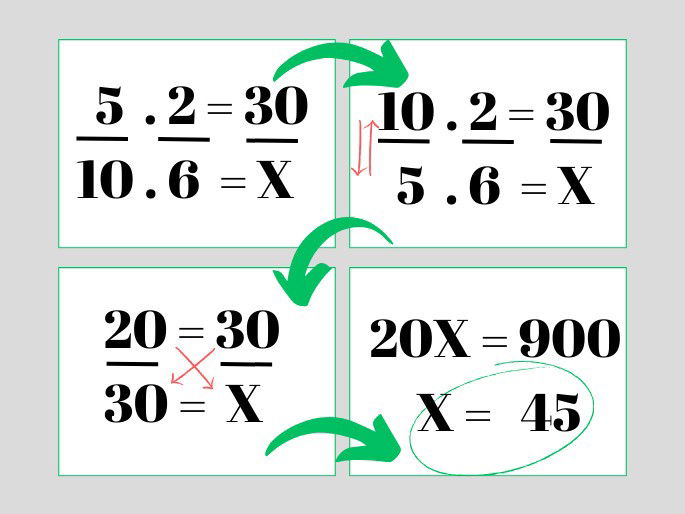
Observe que a grandeza número de pedreiros foi invertida (no segundo quadro), isso acontece porque devemos inverter a grandeza que é inversamente proporcional para fazer a regra de 3 composta corretamente.
Resposta: 10 pedreiros construirão 6 casas em 45 dias.
Veja também: o que é o metro quadrado e como calcular, método da soma e do produto e a tabuada completa.
