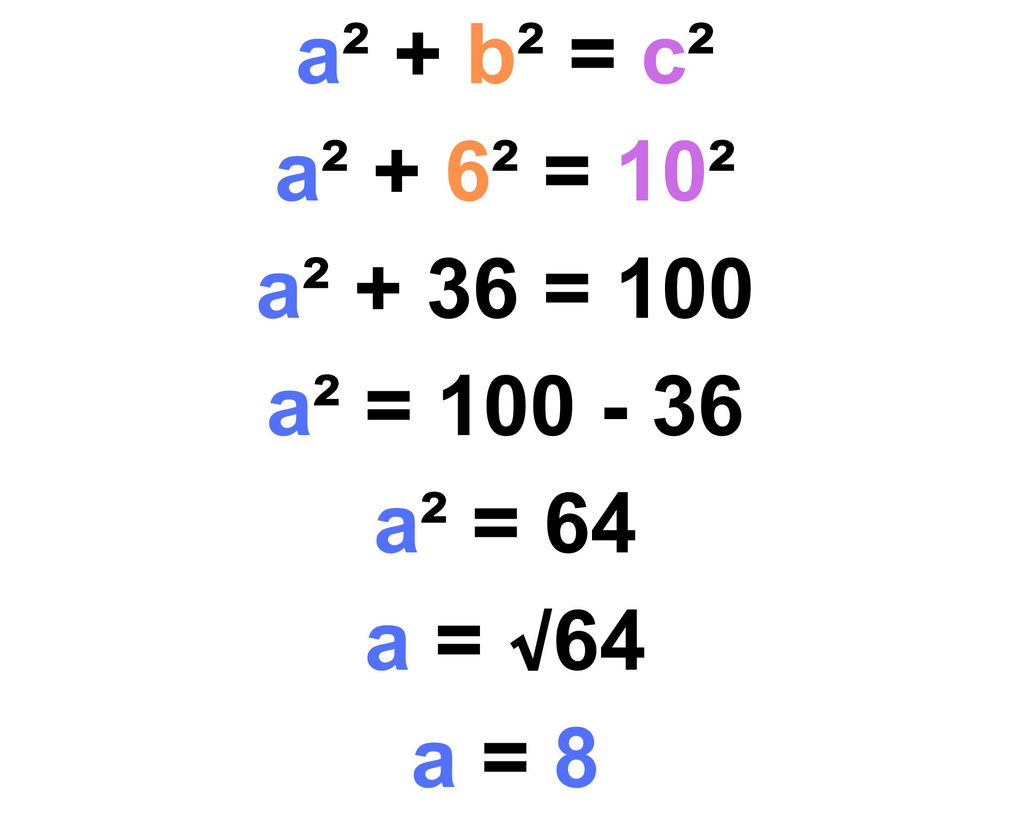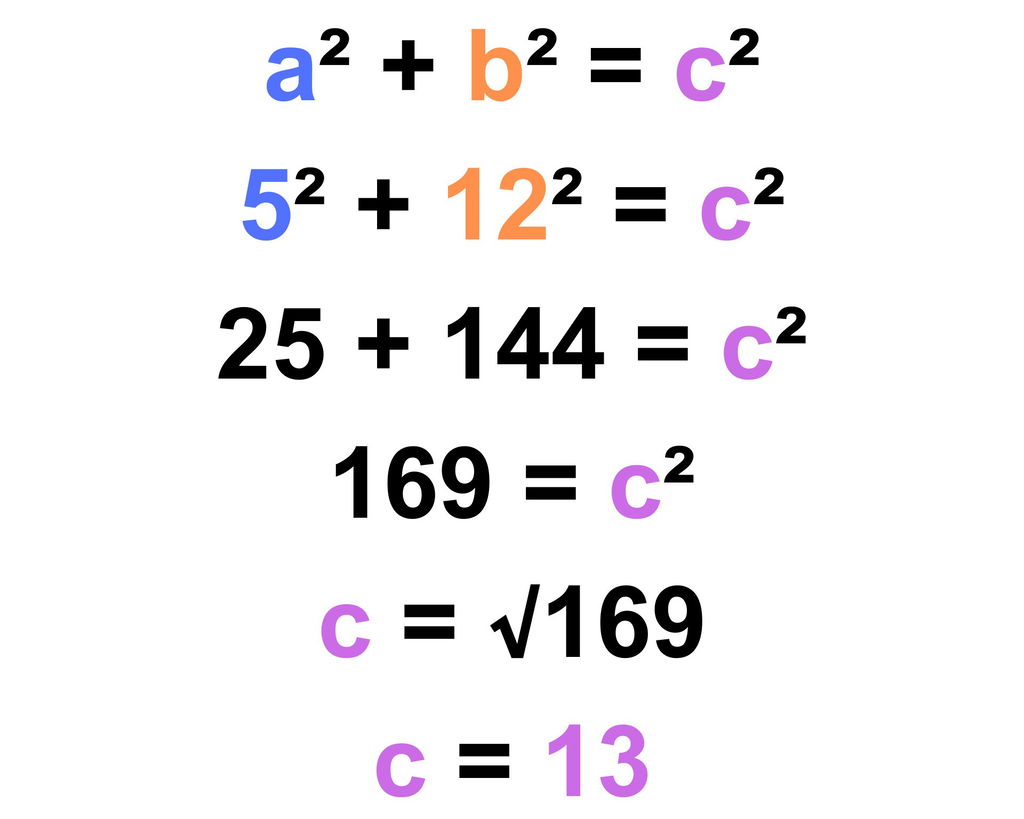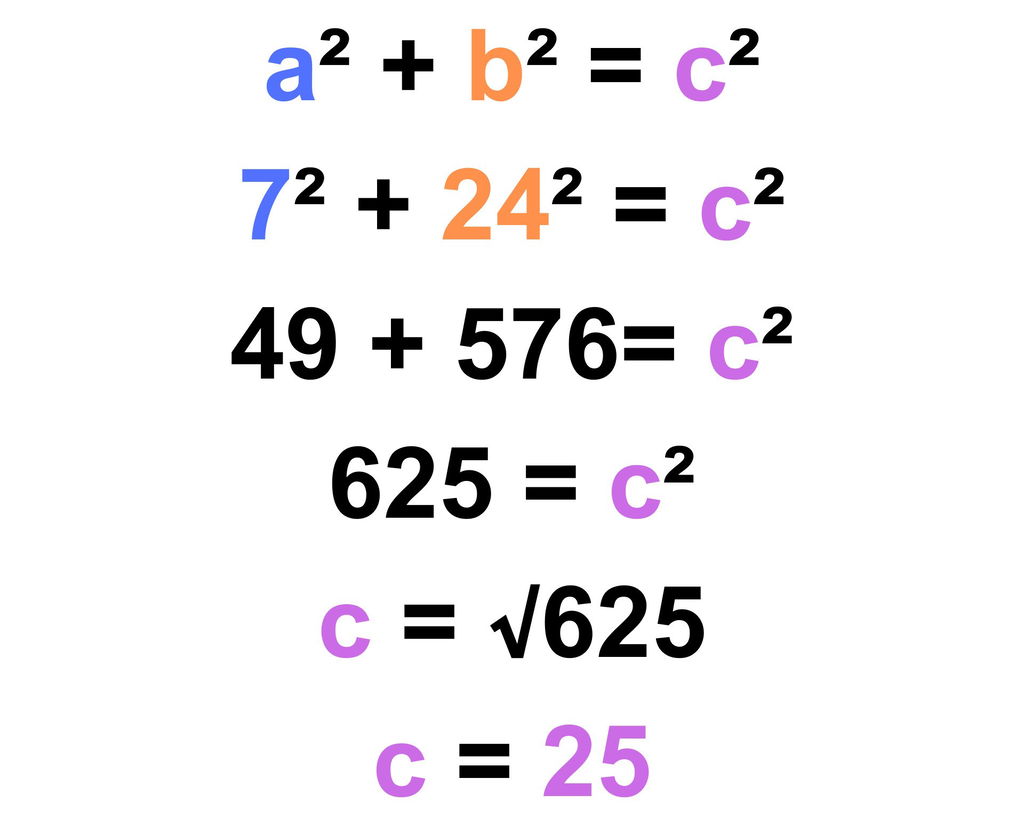Teorema de Pitágoras

Revisão por Rafael C. Asth

Professor de Matemática e Física

Teorema de Pitágoras é um princípio da geometria matemática que afirma a relação entre os comprimentos dos lados do triângulo retângulo.

O princípio diz que "o quadrado da hipotenusa é igual a soma dos quadrados dos catetos". Hipotenusa e catetos são os nomes dados aos lados do triângulo.

O Teorema de Pitágoras somente pode ser usado em triângulos retângulos. Um triângulo retângulo é aquele que possui um ângulo reto, ou seja, um ângulo de 90º.

Conheça a fórmula do Teorema de Pitágoras:

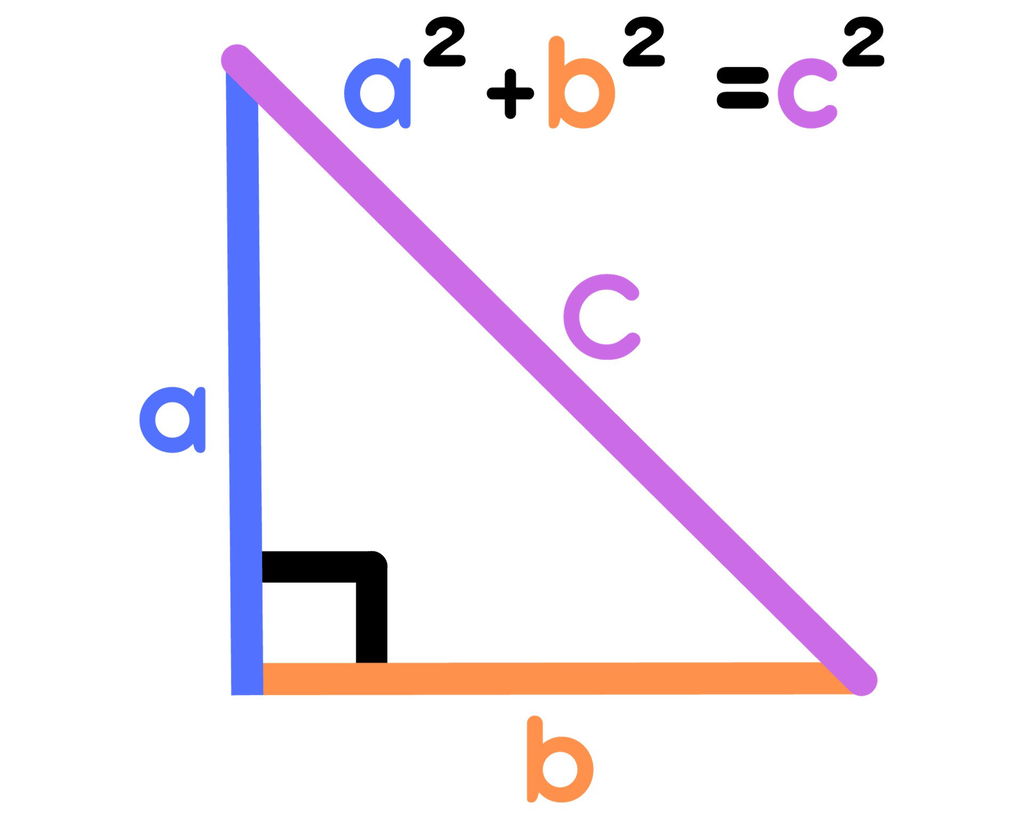
Na fórmula, A e B são os catetos do triângulo e C é a hipotenusa.

Como calcular o Teorema de Pitágoras

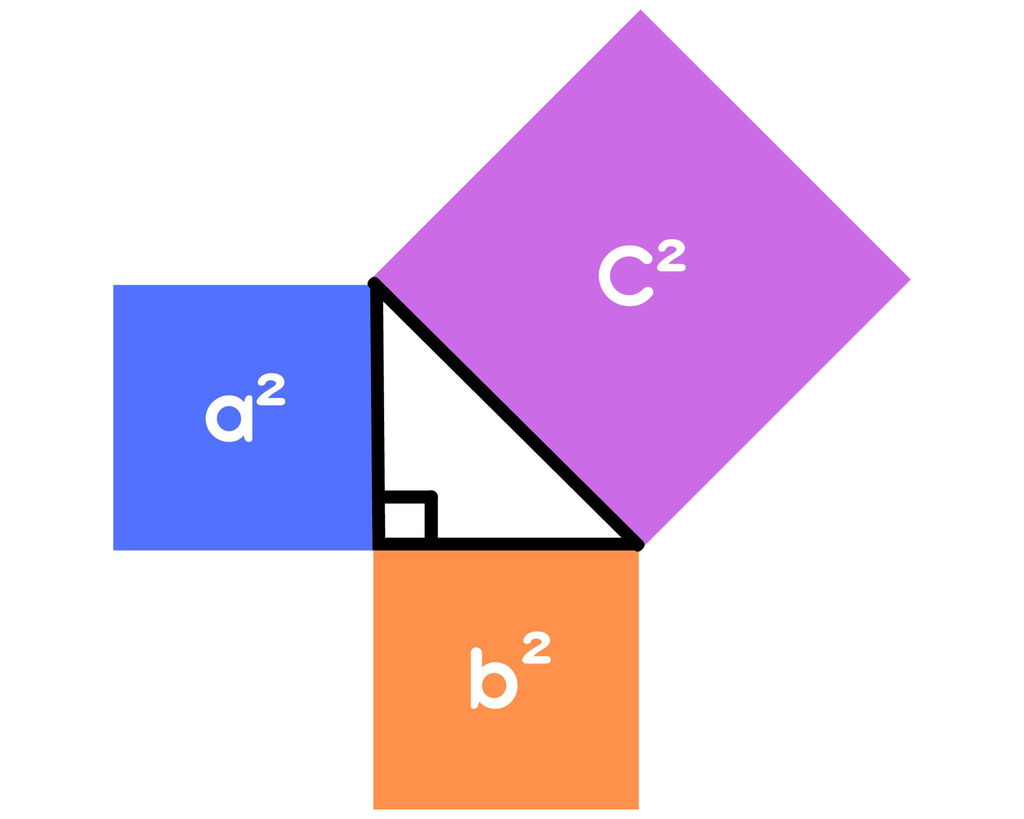
O Teorema de Pitágoras é usado para descobrir o valor de um dos lados do triângulo retângulo, quando se conhece os outros dois lados. A fórmula apresenta que elevar o valor dos dois catetos ao quadrado tem como resultado o quadrado do valor da hipotenusa.

A partir da fórmula a²+b²=c², em que a e b são os catetos e c é a hipotenusa, consegue-se achar o valor desconhecido. Vamos supor que a = 4 e b = 3, qual seria o valor de c? Entenda como é feito o cálculo:

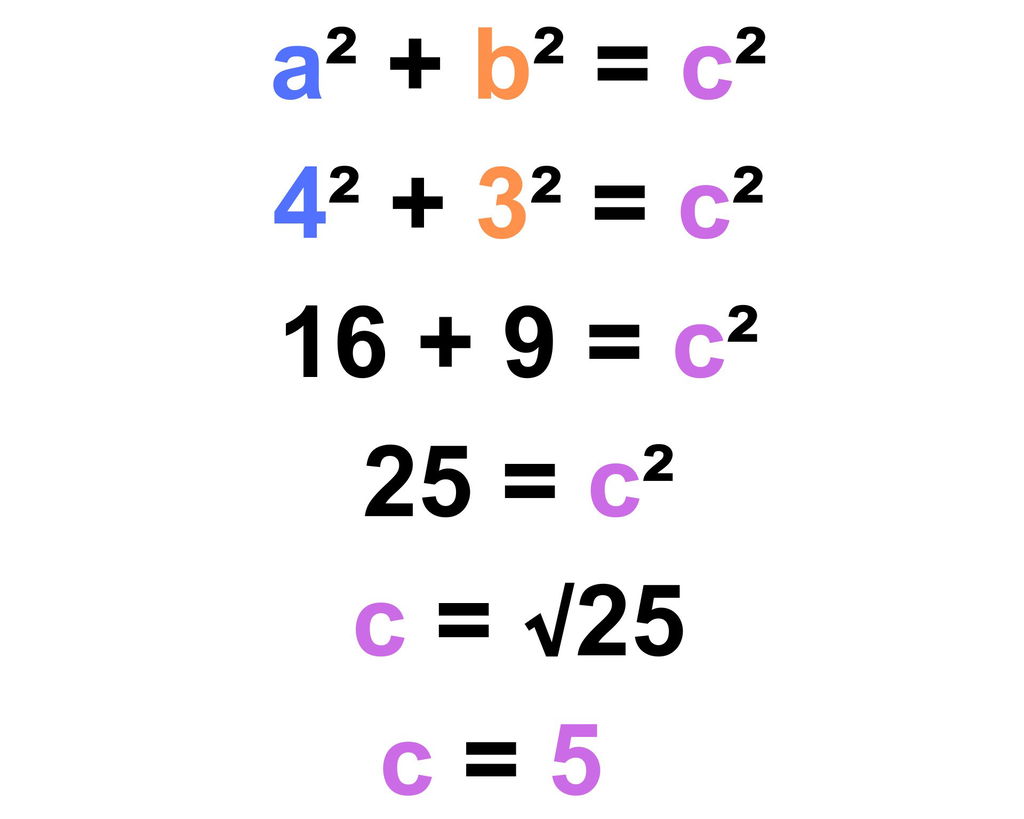
Os valores conhecidos de a e b são substituídos na fórmula por 4 e 3, respectivamente. Então, elevam-se esses números ao quadrado, no qual multiplicamos o número por ele mesmo, 4x4=16 e 3x3=9. Em seguida, soma-se os valores encontrados de 16 e 9, resultando em 25.

Esse valor, 25, é igual a C ao quadrado, para se descobrir o valor real de C é necessário fazer a raiz quadrada de 25, que é 5. Logo C é igual a 5. Em resumo, nesse pequeno problema, temos o cateto a = 4, o cateto b = 3 e a hipotenusa = 5.

Hipotenusa e Catetos

Vale lembrar que os catetos são os lados do triângulo que compõe o ângulo de 90º, o ângulo reto interno. Já a hipotenusa é o lado oposto ao ângulo de 90º, é o maior lado do triângulo retângulo.

Conheça também os tipos de triângulos.

Exemplos de uso do Teorema de Pitágoras

Veja outros exemplos para entender melhor o Teorema de Pitágoras:

Exercícios para descobrir um dos catetos

1. Em um triângulo retângulo, a hipotenusa tem 10 cm de comprimento e um dos catetos: 6 cm, qual é o tamanho do outro cateto?
   
   
   Resposta: O outro cateto mede 8 cm.
2. A hipotenusa de um triângulo retângulo é 15 e um dos catetos é 9, qual é o comprimento do segundo cateto?
   
   
   
   Resposta: O segundo cateto tem o comprimento de 12.

Veja também a tabuada completa.

Exercícios para descobrir a hipotenusa

1. Na fórmula do Teorema de Pitágoras, a e b representam os catetos e c presenta a hipotenusa.Um triângulo retângulo tem a = 5 e b =12, qual é o comprimento da c?
   
   
   Reposta: O comprimento de c é 13.
2. Um terreno tem a forma de um triângulo retângulo. Um agricultor precisa calcular o comprimento da hipotenusa para determinar a quantidade de material necessário para cercar o terreno. Ele mediu os catetos e encontrou que a = 7 metros e b = 24 metros. Qual é o comprimento da hipotenusa?
   
   
   Resposta: A hipotenusa do terreno tem 25 metros.

História do Teorema de Pitágoras

O Teorema de Pitágoras leva o nome de seu criador. Pitágoras teria nascido na Grécia Antiga, em Samos, no ano de 569 a.C. Foi um grande pensador pré-socrático, criador do pitagorismo, que influenciou a filosofia e a matemática.

Filho de comerciantes, Pitágoras teria tido a oportunidade de receber uma boa educação e viajar por vários territórios, entrando em contato com diversos povos e suas formas de usar a matemática. Sabe-se que o Pitágoras viveu no Egito, acredita-se também que tenha chegado à Índia e à Arábia.

Já mais velho, Pitágoras se fixou e se dedicou somente ao conhecimento, fundando sua escola pitagórica de pensamento, que tinha como base a ideia de que o mundo era formado por números. Teve centenas de estudiosos e seguidores.

Acredita-se que nesse período tenha formulado o Teorema de Pitágoras, entretanto não existem documentos escritos pelo matemático, o que se conhece sobre o seu trabalho foi resultado da comunicação oral e dos registros de seus seguidores.

Saiba também: como fazer a regra de 3 e reconhecer números primos.