Números primos
Os números primos são números naturais que tem apenas dois divisores positivos: o 1 e ele mesmo. Ou seja, para que um número seja primo, ele não pode ser divisível por outro número que não seja o 1 e ele mesmo.
Por exemplo, o número 11 é um número primo. Isso acontece porque não existe outro número (além do 1 e do próprio 11) que divida o 11 e tenha como resultado um número positivo.
Já o número 4 não é um número primo, pois pode ser divido por ele mesmo, pelo 1 e também pelo 2, resultando em um número positivo. Pois 4 ÷ 2 = 2 (quatro divido por dois é igual a dois).
Os números que tem mais de dois divisores são chamados de números compostos. Logo, o 4 é um número composto.
Os números primos são infinitos e são muito usados na matemática, mas também fora dela, em áreas como a criptografia e a computação.
Tabela de números primos
Veja quais números, de 1 a 1000, são primos:
| 2 | 3 | 5 | 7 | 11 | 13 |
| 17 | 19 | 23 | 29 | 31 | 37 |
| 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 |
| 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 |
| 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 |
| 401 | 409 | 419 | 421 | 431 | 433 |
| 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 |
| 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 |
| 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 |
| 751 | 757 | 761 | 769 | 773 | 787 |
| 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 |
| 877 | 881 | 883 | 887 | 907 | 911 |
| 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
É importante ressaltar que o número 1 não é primo. O 1 tem um único divisor, ele mesmo, e para que fosse considerado primo teria que ter dois divisores cujo resultado fosse positivo.
Contudo, também não é considerado número composto, pois para ser composto o 1 teria que ter mais de dois divisores com resultado positivo. Por isso, o 1 não é considerado nem primo, nem composto.
O número 2 é o único número primo que é par. Os outros números primos são todos ímpares.
Como saber se um número é primo
Para que um número seja primo, ele precisa ter somente dois divisores cujo resultado seja positivo: o 1 e ele mesmo. Essa é a principal informação para saber se um número é primo ou não. Também ajuda entender que os números primos são sempre ímpares, com a única exceção do número 2.
Método da divisão
É possível descobrir se um número é primo por meio da divisão. Trata-se de um método baseado na tentativa e erro, que indica que se deve dividir o número (que se quer descobrir se é primo) por todos os números primos menores ou iguais a sua raiz quadrada.
Por exemplo: queremos saber se o número 29 é primo. Primeiro é necessário calcular a raiz quadrada de 29, que não é um número exato, portanto, temos um resultado aproximado, √29 ≅ 5,385.
Então, verificamos quais são os números primos abaixo de 5,385. São eles 2, 3 e o 5. Fazemos as divisões:
- 29 ÷ 2 = 14,5 (não é um número inteiro)
- 29 ÷ 3 = 9,6 (não é um número inteiro)
- 29 ÷ 5 = 5,8 (não é um número inteiro)
Concluímos que 29 é um número primo, pois não é divisível por nenhum dos números primos abaixo do valor da sua raiz quadrada.
Em outro exemplo, queremos descobrir se o número 81 é primo. Verificamos a raiz quadrada de 81, √81 = 9. Os números primos menores do que nove são: 2,3,5 e 7. Então, dividimos:
- 81 ÷ 2 = 40,5 (não é um número inteiro)
- 81 ÷ 3 = 27 (número inteiro)
- 81 ÷ 5 = 16,2 (não é um número inteiro)
- 81 ÷ 7 = 11,5 (não é um número inteiro)
Observando os resultados das divisões, vemos que 81 é divisível por 3. Isso quer dizer que tem mais do que dois divisores (1 e ele mesmo), por isso, não é um número primo.
Saiba como fazer a raiz quadrada.
Crivo de Eratóstene
Outra forma de descobrir os números primos é chamado Crivo de Eratóstene. Esse método foi desenvolvido pelo matemático de mesmo nome, que viveu na Alexandria, por volta de 276 a.C.
O método consiste em listar os todos os números de 1 até aquele que se desejar verificar. Por exemplo: do 1 ao 100. Faz-se, então, o descarte dos múltiplos dos números primos.
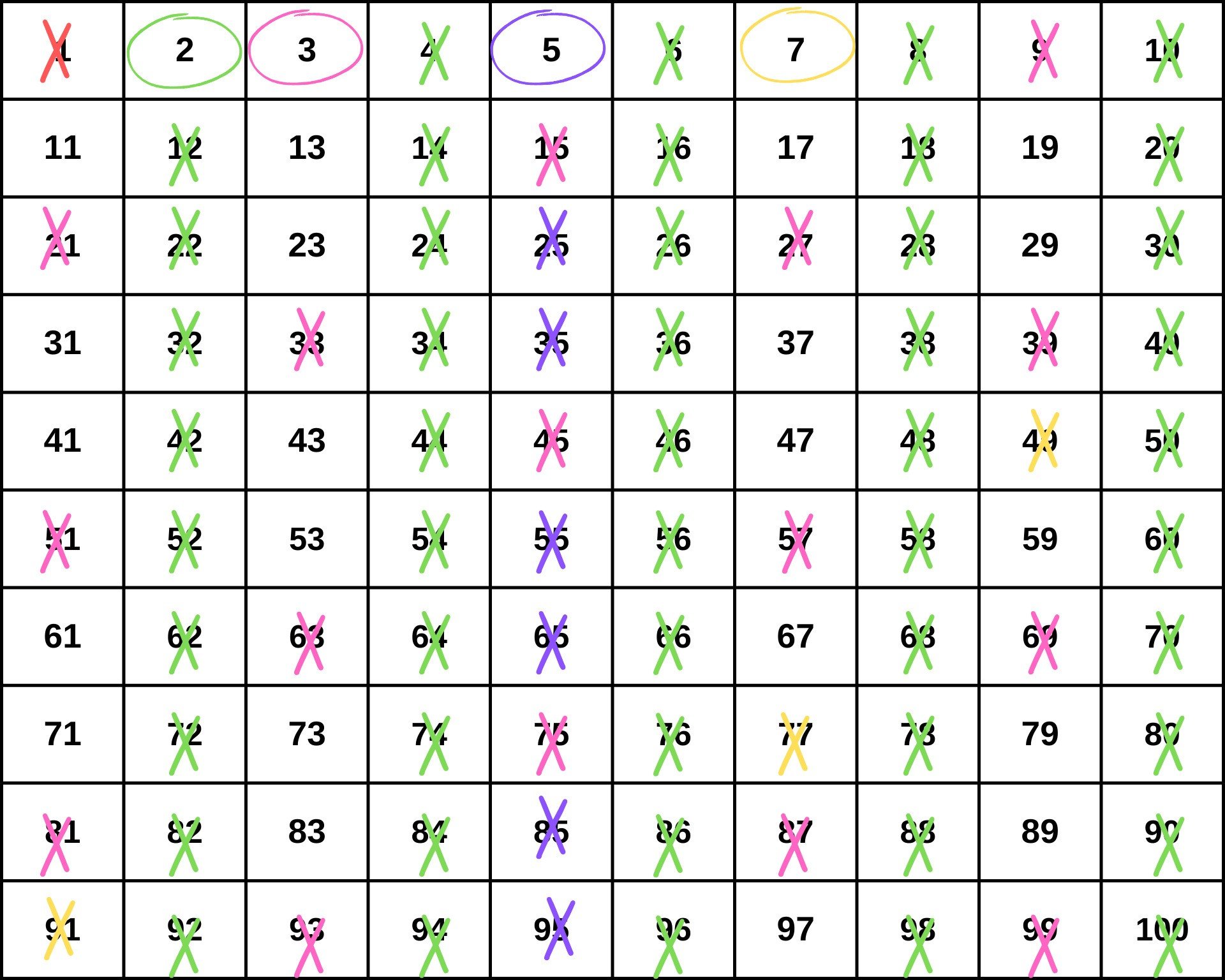
Na primeira linha, temos os primos 2, 3, 5 e 7. Lembre-se que o número 1 não é primo, nem composto, por isso, é já retirado da lista (em vermelho).
Depois se retira todos os múltiplos de 2 (em verde), note que ao retirar os múltiplos de 2, descarta-se todos os números pares. Por isso, o 2 é o único número par que é também primo.
Em seguida, retira-se todos os múltiplos de 3 (em rosa). É importante saber a tabuada para poder trabalhar com o Crivo de Erastótene. Posteriormente, descartam-se os múltiplos de 7 (em amarelo). Os números restantes, que não foram excluídos, são todos primos.
Esse método também pode ser usado para conhecer números primos maiores, bastaria criar uma lista mais longa com todos os números e seguir a mesma linha de raciocínio, eliminando os múltiplos dos números primos.
Veja também: